(a) Explain in what respect, the process of ‘analysing a problem’ and ‘analysing an algorithm’ are essential for developing computer-based solutions of problems.
(b) Show that an = O (bn), where a and b are some constant natural numbers. (5 marks)
(c) Solve the following inhomogeneous recurrence.
G (m) – 7 G(m – 1) + 12 G (m – 2) = 9.
(d) Suggest some method of computing x1218792, where x is a natural number, and the method does not use more than 2 log2(1218792) number of product operations.
Q2:
(a) Sort the following list in increasing order of numbers
9, 94, 45, 47, 28, 98, 65, 42, 78, 4, 11, 88, 6
using each of the following methods,
(i) Merge Sort
(ii) Quick Sort
(iii) Insertion Sort
(iv) Selection Sort
(v) Heap Sort
Further, count the number of operations, by each sorting method.
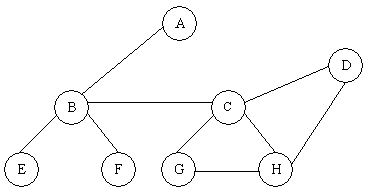
(b) For the graph given below, use DFS to visit various vertices taking C as starting vertex.
Q3:
Multistage Graphs Problem:
A multistage graph G = (V, E) is a directed graph in which the vertices are partitioned in k ³ 2 disjoint sets say V1, V2, ………, Vk. Further, if (u, v) is an edge in E, then, for i with 1 £ i < k, the edge u belongs to Vi and the vertex v belongs to Vi+1. The number of vertices in each of the first and last sets viz., V1 and Vk is one. Let the node in the first set V1 be called s and the node in the last set Vk be called t. Further, let c(i, j) be the cost of traversing from vertex i to vertex j.
The Multistage Graph Problem is to find a minimum cost path from the start node s to the terminal node t. Using Dynamic Programming, suggest a solution to Multi-stage Graph Problem.
