Ans. Search is one of the operational tasks that characterize AI programs best. Almost every AI program depends on a search procedure to perform its prescribed functions. Problems are typically defined in terms of states, and solutions correspond to goal states. Solving a problem amounts to searching through the different states until one or more of the goal states are found. Search is ubiquitous to AI. For every problem there are numerous alternatives to consider:

• When attempting to understand a natural language, a program must search to find matching words that are known, sentence construction, and matching contexts.
• In vision perception, program searches must be performed to find model patterns that match input scenes.
• In theorem proving, clauses must be found by searching axioms and assertions which resolve together to give the empty clause. This requires a search of literals which unify and then a search to find resolvable clauses

This problem consists of a 3 by 3 square frame which holds eight movable squares tiles which are numbered from 1 to 8. One square is empty, permitting tiles to be shifted. The objective of the puzzle is to find a sequence of tile movements that leads from a starting configuration to a goal configuration as shown in the following figure:

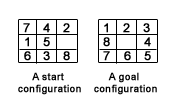
The states of the eight puzzle are different permutations of the tiles within the frame. The operations are permissible moves: up, down, left, and right. An optimal solution maps the initial configuration to the goal configuration with the smallest number of moves. The following figure depicts the search space for the problem.

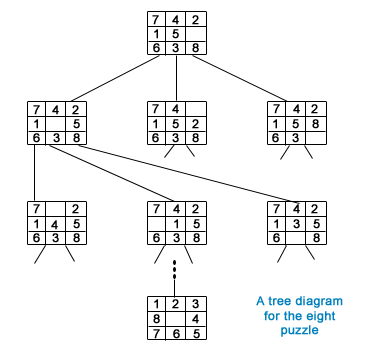
In the above figure, the nodes are depicted as puzzle configurations. The root node represents a randomly chosen starting configuration, and its successor nodes correspond to the three single tile movements that are possible from the root. A path is a sequence of nodes starting from the root and progressing to the goal node.