|
Breadth-first searches are performed by exploring all nodes
at a given depth before proceeding to the next level. This
means that all immediate children of nodes are explored before
any of the children's children are considered .Breadth first
tree search is illustrated below:
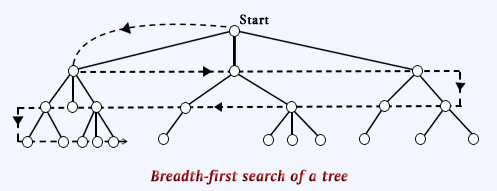
It has the obvious advantage always finding a minimal path
length solution when one exists. However, a great many nodes
may need to be explored before a solution is found, especially
if the tree is very full.
An algorithm for the breadth-first search is quite simple.
It uses a queue structure to hold all generated but still
unexplored nodes. The order in which nodes are placed on the
queue for removal and exploration determines the type of search.
The breadth-first algorithm is paraphrased below:
1. Place the starting node s on the queue.
2. If the queue is empty, return failure and stop.
3. If the first element on the queue is a goal node g,
return success and stop. Otherwise ,
4. Remove and expand the first element from the queue and
place at the end of the queue in any order .
5. Return to step 2.
The time complexity of this algorithm is O(bd)
because all nodes to the goal depth d are generated. The space
complexity is also O(bd) because all nodes at a
given depth must be stored in order to generate the nodes
at the next depth. The use of both exponential time and space
is one of the main drawbacks of the breadth-first search.
|
