|
Hill Climbing Methods
| Q. Discuss briefly some the potential problems when
using hill climbing search. (Dec. 01, Dec. 02) |
|
Ans. Hill climbing is like depth-first searching where
the most promising child is selected for expansion. When the
children have been generated, alternative choices are evaluated
using some type of heuristic function. Hill climbing can produce
substantial savings over blind searches when an informative,
reliable function is available to guide the search to a global
goal. It suffers from some serious drawbacks when this is
not the case. Potential problem types named after certain
terrestrial anomalies are:
- Foothill trap: The foothill trap results when local maxima
or peaks are found. In this case the children all have less
promising goal distances than the parent node. The search
is essentially trapped at the local node with no indication
of goal direction.
- Ridge: This problem occurs when several adjoining nodes
have higher values than surrounding nodes. This is the equivalent
of a ridge.
- Plateau traps: The search may encounter a plateau type
of structure, that is, an area in which all neighboring
nodes have the same values.
|
Best First Search
| Best-First Search (June 01, June 02, Dec. 02) |
|
The Best-first search depends on the use of a heuristic to
select most promising paths to the goal node. This algorithm
retains all estimates computed for previously generated nodes
and makes its selection base on the best among them all. Thus,
at any point in the search process, best-first moves forward
from the most promising of all the nodes generated so far.
In doing so, it avoids the potential traps encountered in
hill climbing" The best-first process is illustrated in the
following figure where numbers by the nodes may be regarded
as estimates of the distance or cost to reach the goal node.
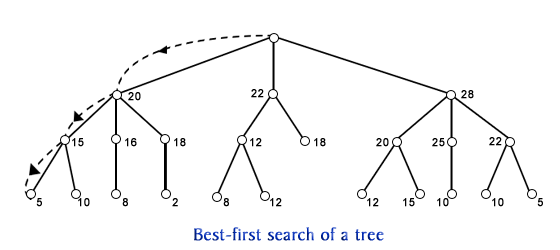
The algorithm is paraphrased below:
- Place the starting node s on the queue.
- If the queue is empty, return failure and stop.
- If the first element on the queue is a goal node g,
return success and stop. Otherwise,
- Remove the first element from the queue, expand it and
compute the estimated goal distances for each child. Place
the children on the queue (at either end) and arrange all
queue elements in ascending order corresponding to goal
distance from the front of the queue.
- Return to step 2.
Best-first searches will always find good paths to a goal,
even when local anomalies are encountered. All that is required
is that a good measure of goal distance be used.
|
Q. Using the search tree given below, list the elements of the
queue just before the next node is expanded. Use best-first serach
where the numbers correspond to estimated cost-to-goal for each
corresponding node. (Dec. 02)


| Expanded Node |
List |
| |
A |
| A |
C B |
| C |
G H B |
| G |
M L H B |
| M |
L H B |
| L |
H B |
| H |
N B |
| B |
F E D |
| E |
K J D |
| K |
J D |
| J |
D |
| D |
I |
| I |
---- |
|
|

