|
Minkowski metric is a general distance measure metric. It
satisfies the following assumption-
For all elements x, y, z, of the set E, the function d is
a metric if and only if
a. d(x, x) = 0
b. d(x, y) ³ 0
c. d(x, y) = d(y, x)
d. d(x, y) £ d(x, z) + d(z,
y)
It is given by
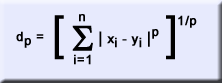
For the case p = 2, this metric is the familiar Euclidean
distance. When p = 1, dp is the so-called absolute
or city block distance.
|