Q. 14. Find the expected value of the number
X shown on the face of a dice, when the dice is thrown.
The dice is unbiased. (Note : Face value of a dice
is 1, 2, 3, 4, 5 or 6) (Jan.
2001)
Solution. X can take values 1,
2, 3, 4, 5, 6 each with a probability 1/6.
E(X) = 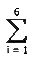 xi P (x = xi)
xi P (x = xi)
or E(X) = [1 X (1/6)] + [2 X (1/6)] + [3 X (1/6)]
+ [4 X (1/6)] + [5 X (1/6)] + [6 X (1/6)]
or E(X) = 3.5
Q. 15. A consignment of eight similar microcomputers
to retail outlet contains 3 that are defective. If
a firm makes a random purchase of 2 of these computers,
find the probability distribution for the number of
defectives. (Dec. 98)
Solution. Let X = random variable (i.e., random
purchase of 2 defective computers)
So, x can take the values (0, 1, 2)
F[X = x = 0] = P[x = 0] = (3C0
X 5C2)/8C2
= 0.36
Therefore, F[x = 0] = 0.36
F[X = x = 1] = P[x = 1] = (3C1
X 5C1)/8C2
= 0.53
Therefore, F[x = 1] = 0.53
F[X = x = 2] = P[x = 2] = (3C2
X 5C0)/8C2
= 0.11
Therefore, F[x = 2] = 0.11
|