|
 y
dx = (h/2) X {(y0 + yn )
+ [2 X (y1 + y2 + y3 +....+
yn-1)]} y
dx = (h/2) X {(y0 + yn )
+ [2 X (y1 + y2 + y3 +....+
yn-1)]}
Q. 7. Evaluate
a) 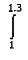 x2
dx (Dec. 99) x2
dx (Dec. 99)
b) I =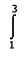 (1
+ x2 + x3) dx (Dec.
2002) (1
+ x2 + x3) dx (Dec.
2002)
using either Simpson's rule or Trapezoidal rule.
Solution. (a)
Using Trapezoidal rule
| x
|
1 |
1.05
|
1.10
|
1.15
|
1.20
|
1.25
|
1.30
|
| y
= x2 |
1 |
1.1025
|
1.21
|
1.3225
|
1.44
|
1.5625
|
1.69
|
Here, h = 0.05, y0 = 1, y1 =
1.1025, y2 = 1.21, y3 = 1.3225,
y4 = 1.44, y5 = 1.5625, y6
= 1.69
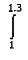 y
dx = (h/2) X {(y0 + y6 )
+ [2 X (y1 + y2 + y3 +
y4 + y5)]} y
dx = (h/2) X {(y0 + y6 )
+ [2 X (y1 + y2 + y3 +
y4 + y5)]}
or 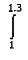 y
dx = (0.05/2) X {(1 + 1.69) + [2 X (1.1025 + 1.21
+ 1.3225 + 1.44 + 1.5625)]} y
dx = (0.05/2) X {(1 + 1.69) + [2 X (1.1025 + 1.21
+ 1.3225 + 1.44 + 1.5625)]}
or 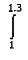 y
dx = 0.3991 y
dx = 0.3991
(b) Using Trapezoidal rule
|
x
|
1
|
2
|
3
|
|
y = (1 + x2
+ x3)
|
3
|
13
|
37
|
Here, h = 1, y0 = 3, y1 = 13,
y2 = 37
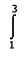 y
dx = (h/2) X [(y0 + y2 ) +
(2 X y1)] y
dx = (h/2) X [(y0 + y2 ) +
(2 X y1)]
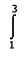 y
dx = (1/2) X [(3 + 37) + (2 X 13)] y
dx = (1/2) X [(3 + 37) + (2 X 13)]
or 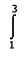 y
dx = 33 y
dx = 33
Q. 8. Compute the approximate value of the
integral
I = (x
+ x2) dx (x
+ x2) dx
using Trapezoidal rule by taking interval size h as
one.
Solution.
| x
|
0 |
1 |
2 |
| y
= (x + x2) |
0 |
2 |
6 |
 y
dx = (1/2) X [(0 + 6) + (2 X 2)] y
dx = (1/2) X [(0 + 6) + (2 X 2)]
or y
dx = 5 y
dx = 5
|