1. (a) Write a FORTRAN 90 statement for each of
the following formulae: (3) (b) Which of the following variable names are
invalid in FORTRAN 90? Justify your answer. (3) (c) Write which of the following FORTRAN constants
are invalid: (3) (d) Suppose the integer variables X and Y contain
respectively 2 and 7. Find the final values of X and
Y in each of the following cases: (3) (e) Suppose at some stage values of integer variables
P, Q and R are respectively 2, 3 and 4. Find the value
of the variable S after each pair of statements given
below: (3) (f) If P, Q and R respectively contain 222.111,
666.444 and 888.777, and the FORTRAN statement (3) (g) The following table gives the height (in inches) of 100 students, randomly selected from a college: (4)
(h) Fit a straight line to the data given by the following table: (4)
2. (a) Write a program in FORTRAN to find whether a given square matrix is symmetric. The program should read the matrix size, the elements of the matrix and also should print out an appropriate message. (9) (b) Write a FORTRAN function FACT with one integer parameter N, that computes the factorial of N and prints suitable message. (6) 3. (a) The constant p can be approximated by (8) p2/6
= (1 + 1/22 + 1/32 + 1/42
+ .......) (b) The following table shows monthly living expenses for an MCA student of IGNOU: (7)
Draw a Pie Chart of the monthly expenses. 4. (a) In a bulb making factory, three machines A, B and C manufacture respectively 15, 35 and 50 percent of the total. Out of their total outputs 4, 5 and 3 percent are defective. A bulb is drawn from the produce at random and is found to be defective. What is the probability that it is manufactured by (i) factory A (ii) factory C? (8) (b) A box contains ten 50-rupee notes, fifteen 10-rupee notes, eighteen 20-rupee notes and twelve 100-rupee notes. A sample of six notes is taken out at random without replacement. Find the probability that the sample contains one 50-rupee note, two 10-rupee notes, one 20-rupee note and two 100-rupee notes. (7) 5. (a) A computer while calculating the correlation
coefficient between 25 pairs of two variables x and
y, obtained the following constants: (8) A recheck showed that the computer has copied wrongly two pairs (6, 14) and (8, 6) of values of (x, y) instead of the correct values (8, 12) and (6, 8) respectively. Obtain the correct value of the correlation coefficient. (b) The following table gives the average wholesale prices of the four fruits for the years 1996 to 2000. Compute chain base index number. (7)
(b) From the following table of values of x and y, obtain dy/dx for x = 1.2. (8)
|
| |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Main Contents Page | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| © Universal Teacher Publications | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
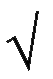 sin2
(xy) + ((x)y)z
sin2
(xy) + ((x)y)z