1. (a) Write a FORTRAN 90 statement for each of
the following mathematical expressions: (3) (b) Which of the following variable names are
invalid in FORTRAN 90? Why or why not? (3) (c) Write which of the following FORTRAN constants
are invalid: (3) (d) Locate the error, if any, in each of the following
WRITE-FORMAT pairs: (3) (e) Suppose integer variables P, Q and R contain
8, 16 and 24 respectively. Find the value of each
of the following logical expressions: (3) (f) Explain the purpose of EQUIVALENCE statement in FORTRAN, giving one appropriate example for the purpose. (3) (g) The following table gives weights (in kilograms) of 100 students, randomly selected from a college: (4)
(h) Fit a straight line to the data given by the following table: (4)
2. (a) Write a FORTRAN function SUMM with one integer parameter N, that computes the sum of first N natural numbers and prints a suitable message. (6) (b) Write a FORTRAN subroutine MMM that computes the mean, the minimum and the maximum of an array A of N real numbers, and prints out the values with suitable messages. (9) 3. (a) Write a FORTRAN program which finds and prints all four-digit prime numbers. (7) (b) For a frequency distribution of marks in History of 200 candidates, the mean and standard deviation (s.d.) were found to be 40 and 15 respectively. Later it was discovered that the score 43 was misread as 53 in distribution. Find the correct mean and standard deviation corresponding to the correct distribution. (8) 4. (a) In a bolt factory machines A, B and C manufacture respectively 30, 35 and 35 percent of the total. Out of their total outputs 3, 4 and 3 percent are defective. A bolt is drawn at random and is found to be defective. What is the probability that it is manufactured by (i) factory A (ii) factory B? (8) (b)A jar contains five 50-paisa coins, four one-rupee coins, three two-rupee and four 5-rupee coins. A sample of size 6 (coins) is taken out at random without replacement. Find the probability that the sample contains two 50-paisa coins, two one-rupee coins, one two-rupee coin and one 5-rupee coin. (7) 5. (a) The following table gives the average wholesale prices of the four grains for the years 1997 to 2001. Compute chain base index number. (7)
6. (a) Compute the approximate value of the integral
(b) A portion of a table of sines is given below:
|
| |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Main Contents Page | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| © Universal Teacher Publications | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
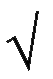 [sin
( x + y2) + tan2 xy]
[sin
( x + y2) + tan2 xy]