Integer Programming

Graphical Method

This section deals with the geometric representation of an integer programming problem. To illustrate the concept of cutting plane method through graphical method, consider again the following problem.

Example

Maximize z = x₁ + 4x₂

subject to
2x₁ + 4x₂ £ 7
5x₁ + 3x₂ £ 15

x₁, x₂ are integers ³ 0

Solution.

First, solve the above problem by applying the simplex method.

After introducing slack variables, we have
2x₁ + 4x₂ + x₃ = 7
or  x₃ = 7 - 2x₁ - 4x₂ ....(i)
5x₁ + 3x₂ + x₄ = 15
or  x₄ = 15 - 5x₁ - 3x₂ ....(ii)

Gomory's constraint
- (1/2x₁ - 3/4 x₃) £ -3/4 ...(iii)

Substituting the value of x₃ in equation (iii).
- 1/2x₁ + 3/4 (7 -2x₁ - 4x₂) £ -3/4
-2x₁ - 3x₂ £ -6 ....(iv)

Gomory's constraint
-1/2x₃ £ -1/2 ....(v)

Substituting the value of x₃ in equation (v)
-1/2 (7 - 2x₁ - 4x₂) £ -1/2
x₁ + 2x₂ £ 3 ....(vi)

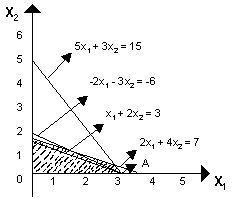
The inclusion of two cuts( -2x₁ - 3x₂ £ -6, x₁ + 2x₂ £ 3) give the new corner point A where x₁ = 3, x₂ = 0 and z = 3