Pure Aloha
The pure Aloha protocol is the basic protocol in the family of the
Aloha protocols. It considers a single-hop system with an infinite
population generating packets of equal length T according to a Poisson
process with rate l packets/sec. The channel is error-free without
capture: whenever a transmission of a packet does not interfere with
any other packet transmission, the transmitted packet is received
correctly while if two or more packet transmissions overlap in time,
a collision is caused and none of the colliding packets is received
correctly and they have to be retransmitted. The users whose packets
collide with one another are called the colliding users. At the end
of every transmission each user knows whether its transmission was
successful or a collision took place. A simple example of the operation
of the protocol is shown below:
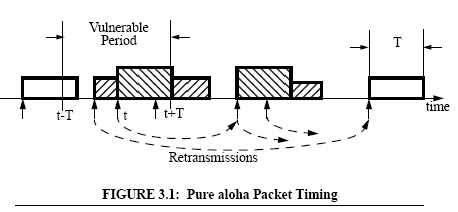
Pure Aloha is a single-hop system. Hence, the throughput is the fraction of time the channel carries useful information, namely noncolliding packets. The channel capacity is the highest value of arrival rate l for which the rate of departure (throughput) equals the total arrival rate.
Consider a packet (new or old) scheduled for transmission at some time t. This packet will be successful if no other packet is scheduled for transmission in the interval (t-T,t+T) (this period of 2T is called the vulnerable period). The probability of this happening, that is, the probability of success, is that no packet is scheduled in an interval of length 2T and since scheduling is Poisson we have
Psuc = e -2gT
Now, packets are scheduled at a rate of g per second of which only a fraction Psuc are successful. Thus, the rate of successfully transmitted packets is gPsuc. When a packet is successful the channel carries useful information for a period of T seconds; in any other case it carries no useful information at all. Using the definition that the throughput is the fraction of time that useful information is carried on the channel we get
S = gTe-2gT
which gives the channel throughput as a function of the offered load. Defining to G gT be the normalized offered load to the channel, i.e., the rate (per packet transmission time) packets are transmitted on the channel, we have
S = Ge-2G
The relation between S and G is depicted in Figure 3.2, which is typical to many Aloha
type protocols. At G=1/2, S takes on its maximal value of 1/(2e0.18
Slotted Aloha
The slotted Aloha variation of the Aloha protocol is simply that of
pure Aloha with a slotted channel. The slot size equals T--the duration
of packet transmission. Users are restricted to start transmission
of packets only at slot boundaries. Thus, the vulnerable period is
reduced to a single slot. In other words, a slot will be successful
if and only if exactly one packet was scheduled for transmission sometime
during the previous slot. The throughput is therefore the fraction
of slots (or probability) in which a single packet is scheduled for
transmission. Because the process composed of newly generated and
retransmitted packets is Poisson we conclude that
S = gTe-gT
or using the definition of the normalized offered load G = gT
S = Ge-G
This relation is very similar to that of pure Aloha, except of increased throughput (see Figure). Channel capacity is 1/ e 0.36 and is achieved at G=1.


