Stepping Stone Method
After computing an initial basic feasible solution, we must now proceed to determine whether the solution so obtained is optimal or not.
Now, we will discuss about the methods used for finding an optimal solution. The Stepping Stone Method is for finding the optimal solution of a transportation problem.
 Steps in Stepping Stone Method: Transportation Problem
Steps in Stepping Stone Method: Transportation Problem
The algorithm is as follows:
1. Determine an initial basic feasible solution using any one of the following:
2. Make sure that the number of occupied cells is exactly equal to m+n-1, where m is the number of rows and n is the number of columns.
3. Select an unoccupied cell. Beginning at this cell, trace a closed path, starting from the selected unoccupied cell until finally returning to that same unoccupied cell.
4. Assign plus (+) and minus (-) signs alternatively on each corner cell of the closed path just traced, beginning with the plus sign at unoccupied cell to be evaluated.
5. Add the unit transportation costs associated with each of the cell traced in the closed path. This will give net change in terms of cost.
6. Repeat steps 3 to 5 until all unoccupied cells are evaluated.
7. Check the sign of each of the net change in the unit transportation costs. If all the net changes computed are greater than or equal to zero, an optimal solution has been reached. If not, it is possible to improve the current solution and decrease the total transportation cost, so move to step 8..
8. Select the unoccupied cell having the most negative net cost change and determine the maximum number of units that can be assigned to this cell. The smallest value with a negative position on the closed path indicates the number of units that can be shipped to the entering cell. Add this number to the unoccupied cell and to all other cells on the path marked with a plus sign. Subtract this number from cells on the closed path marked with a minus sign.
For clarity of exposition, consider the following transportation problem.
 Example 1: Stepping Stone Method
Example 1: Stepping Stone Method
A company has three factories A, B, and C with production capacity 700, 400, and 600 units per week respectively. These units are to be shipped to four depots D, E, F, and G with requirement of 400, 450, 350, and 500 units per week respectively. The transportation costs (in Rs.) per unit between factories and depots are given below:
| Depot | |||||
|---|---|---|---|---|---|
| Factory | D | E | F | G | Capacity |
| A | 4 | 6 | 8 | 6 | 700 |
| B | 3 | 5 | 2 | 5 | 400 |
| C | 3 | 9 | 6 | 5 | 600 |
| Requirement | 400 | 450 | 350 | 500 | 1700 |
The decision problem is to minimize the total transportation cost for all factory-depot shipping patterns.
Solution.
An initial basic feasible solution is obtained by Matrix Minimum Method and is shown below in table 1.
Table 1
| Depot | |||||
|---|---|---|---|---|---|
| Factory | D | E | F | G | Capacity |
| A | 4 | |
8 | |
700 |
| B | |
5 | |
5 | 400 |
| C | 9 | 6 | |
600 | |
| Requirement | 400 | 450 | 350 | 500 | 1700 |
Here, m + n - 1 = 6. So the solution is not degenerate.
Initial basic feasible solution
6 X 450 + 6 X 250 + 3 X 50 + 2 X 350 + 3 X 350 + 5 X 250 = 7350
Table 2
The cell AD (4) is empty so allocate one unit to it. Now draw a closed path from AD. The result of allocating one unit along with the necessary adjustments in the adjacent cells is indicated in table 2.

The increase in the transportation cost per unit quantity of reallocation
is
+4 – 6 + 5 – 3 = 0.
This indicates that every unit allocated to route AD will neither increase nor decrease the transportation cost. Thus, such a reallocation is unnecessary.
Choose another unoccupied cell. The cell BE is empty so allocate one
unit to it.
Now draw a closed path from BE as shown below in table 3.
Table 3
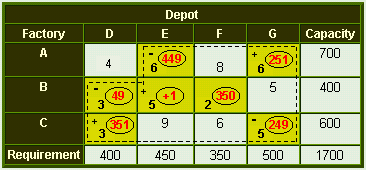
The increase in the transportation cost per unit quantity of reallocation
is
+5 – 6 + 6 – 5 + 3 – 3 = 0
This indicates that every unit allocated to route BE will neither increase nor decrease the transportation cost. Thus, such a reallocation is unnecessary.
We must evaluate all such unoccupied cells in this manner by finding closed paths and calculating the net cost change as shown below.
| Unoccupied cells | Increase in cost per unit of reallocation | Remarks |
|---|---|---|
| CE | +9 – 5 + 6 – 6 = 4 | Cost Increases |
| CF | +6 – 3 + 3 – 2 = 4 | Cost Increases |
| AF | +8 – 6 + 5 – 3 + 3 – 2 = 5 | Cost Increases |
| BG | +5 – 5 + 3 – 3 = 0 | Neither increase nor decrease |
Since all the values of unoccupied cells are greater than or equal to zero, the solution obtained is optimal.
Minimum transportation cost is:
6 X 450 + 6 X 250 + 3 X 50 + 2 X 350 + 3 X 350 + 5 X 250 = Rs. 7350
Confused!!!  "Furious activity is no substitute
for understanding."
"Furious activity is no substitute
for understanding."



