Dual Formulation: Linear Programming
In this section, we will introduce the concept of Dual Formulation in Linear Programming (LP). Now lets concentrate on the following example:
 Example: Dual Formulation in Linear Programming
Example: Dual Formulation in Linear Programming
Minimize z = 3x1 + 3x2
subject to
2x1 + 4x2 ≥
40
3x1 + 2x2 ≥ 50
x1, x2 ≥ 0
Solution.
Maximize z = 40w1 + 50w2
subject to
2w1 + 3w2 ≤
3
4w1 + 2w2 ≤ 3
w1, w2 ≥ 0
Primal Dual Relationship in Linear Programming (LP)
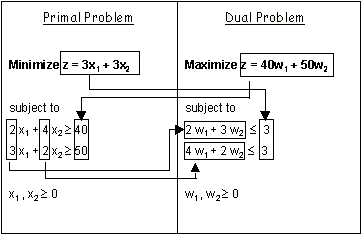
Primal Dual Relationship
- The number of constraints in the primal problem is equal to the number of dual variables, and vice versa.
- If the primal problem is a maximization problem, then the dual problem is a minimization problem and vice versa.
- If the primal problem has greater than or equal to type constraints, then the dual problem has less than or equal to type constraints and vice versa.
- The profit coefficients of the primal problem appear on the right-hand side of the dual problem.
- The rows in the primal become columns in the dual and vice versa.



